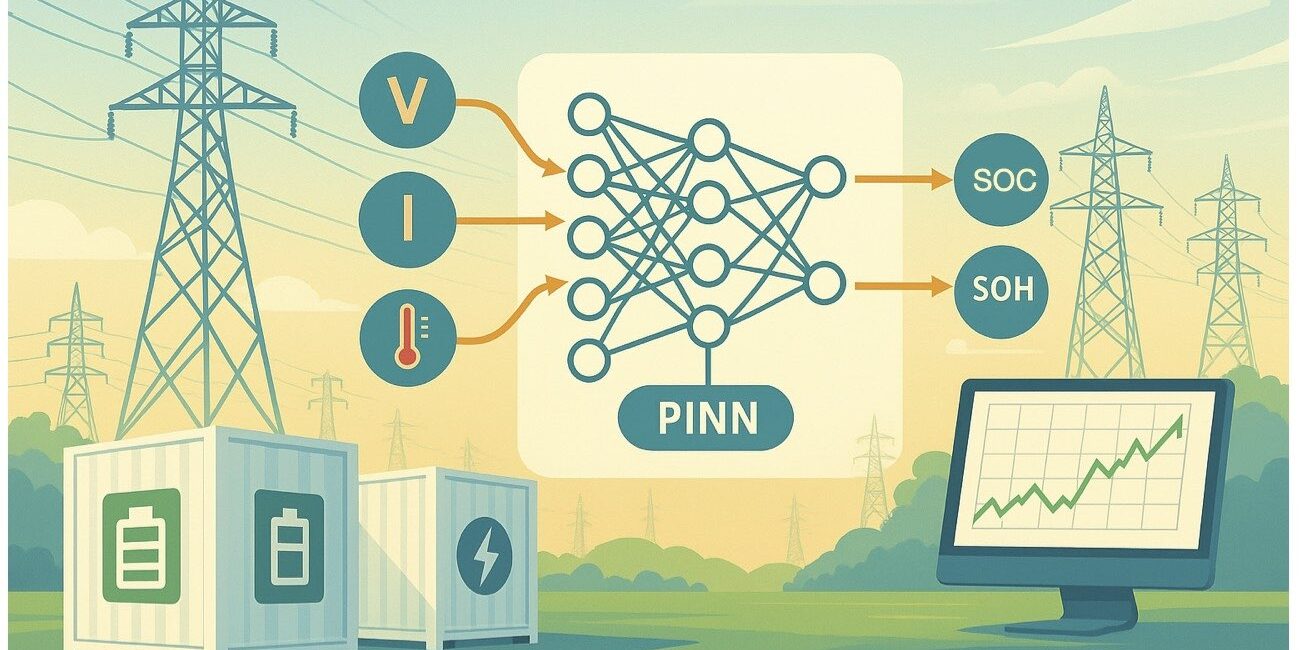
A Physics-Informed Neural Network (PINN) is a machine learning architecture designed to solve scientific problems by harmonizing data with physical laws. Its core innovation lies in training a neural network not only to fit observed data but also to adhere to known governing equations, typically ordinary or partial differential equations. This is achieved by incorporating the residuals of these equations directly into the loss function. Boundary and initial conditions are also added to this function. The network uses automatic differentiation to compute the precise derivatives required for these calculations. While the concept of neural network-based differential equation solvers originated in the 1990s, the modern framework and the term PINN were popularized by Raissi, et al. between 2017 and 2019 [1].
The principal advantage of this approach is that embedded physics acts as a powerful regularizer, ensuring predictions obey conservation laws and other constraints. This is particularly valuable in scenarios where data is scarce, noisy, or expensive to obtain. The PINN framework is uniquely flexible. It is capable of tackling both forward problems, such as simulating system states, and inverse problems, such as inferring unknown parameters, all within a unified structure.
This capability is proving transformative for managing grid-connected battery storage systems. Here, PINNs integrate real world operational data with first principles electrochemical and thermal models. This synthesis allows them to generate physically consistent, trustworthy estimates and forecasts. They accurately infer critical states like State of Charge (SOC) and State of Health (SOH), track degradation trajectories, and act as the core for digital twins that monitor assets in real time. By translating forecasts for energy demand, renewable generation, and market prices into operational strategies, PINNs enable charge/discharge schedules that rigorously respect power, energy, and thermal constraints while explicitly accounting for battery aging.
The practical achievements are promising. Academic research has demonstrated that PINNs can deliver accurate and stable SOH estimation using real cycling data [2]. On the applied front, national laboratories and industry teams are piloting PINN-based surrogate models that accelerate health diagnostics by orders of magnitude; a notable NREL announcement highlighted a model nearly 1,000 times faster than conventional methods. This leap in speed is crucial for scalable fleet monitoring and faster market facing analytics for utilities and aggregators.
Looking ahead, the vision is for physics-aware digital twins powered by PINNs to become standard tools. These models would sit alongside traditional forecasters, enabling degradation-aware bidding, arbitrage, and reserve offers. For asset owners, this integration promises significant improvements. These include more reliable revenue and lifetime projections, along with tighter safety margins. It also facilitates faster online estimation and stronger risk assessments. A major advantage is that all of this is possible without the need to disclose proprietary design details.
Significant hurdles remain to full deployment. These include ensuring model robustness across diverse battery chemistries and temperatures. Another challenge is scaling effectively from single cells to entire packs and fleets. Researchers must also overcome data sparsity and quality issues. Finally, solutions must meet the stringent real time constraints and regulatory expectations of grid operations. Addressing these challenges is the current focus of ongoing research in physics-ML integration for energy storage.
[1] Raissi, M., Perdikaris, P. and Karniadakis, G.E., 2019. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. Journal of Computational physics, 378, pp.686-707.
[2] Wang, F., Zhai, Z., Zhao, Z., Di, Y. and Chen, X., 2024. Physics-informed neural network for lithium-ion battery degradation stable modeling and prognosis. Nature Communications, 15(1), p.4332.